円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 楕円の面積 楕円扇形の面積 楕円弓形の面積 放物線の弓形 双曲線弓形の面積 双曲線扇形の面積 地図をなぞって面積を計算面積の計算方法について ※面積は、カットパスの中で最も広い部分の、縦と横を掛けた総面積で計算します。 例: 「縦12cm、横12cm」 の 「円」 の場合、 「12cm×12cm」 で 「144cm 2 」 となりますので、 この場合は弊社価格表の 「150平方cm以下」 が該当します。・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。 ・扇形の面積 半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。
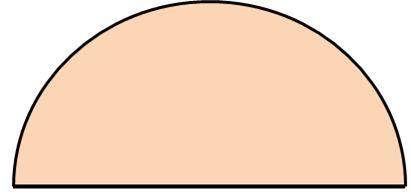
半円や4分の1の円 四分円 の面積を計算する方法 モッカイ
円 面積 一部 計算
円 面積 一部 計算-A=面積 P=楕円の周囲 A=πab 、Pを求める近似式 A=面積 A=面積BCD A=面積 なお点線に示すよう二つの三角形となし 各々の面積を計算しその和をもって 不平行四辺形の面積を算出してもよい =弧の長さ xがyに比し小なる場合の近似式 または A=面積 R=外接円の半径半径rの値を入力し「円の面積を計算」ボタンをクリックすると、半径から円の面積と周囲の長さを計算して表示します。 半径 r: 半径が1の円の面積



円 の面積 計算ドリル 問題集 数学fun
これで、 円の面積がπに半径( 上の例では、1)の二乗をかけたものであることが 証明できました(変換式のsin、cosの前にrを付ければ、円の面積はπr 2 となる )。 次に、数値積分の方法を使って円の面積を計算してみます(図2参照)。円の面積の公式は思い出せましたか。 思い出せない方は、円の面積はパイ・アールの2乗と覚えてください。 なお、パイとは円周率のことで314、アールとは円の半径のことなので、記号を使って表わすと、 円の面積=314×r×r球の体積基準比表面積(単位体積当たりの表面積) \(\displaystyle \frac {6}{D}\) 球の質量基準比表面積(単位質量当たりの表面積) \(\displaystyle \frac {6}{D \rho}\) 半分以上隠れている円の直径の推定 接触角の概算 円と球の空間
円の面積 円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 楕円の面積 楕円扇形の面積 楕円弓形の面積 放物線の弓形 双曲線弓形の面積 双曲線扇形の面積 地図をなぞって面積を計算扇形面積=円の面積×( 扇の内角/360°) 三角形の面積=( 半径2×sin扇の内角 )/2 ・・・二辺夾角法円の面積=4cm×4cm×314=5024cm 2 円の円周=4cm×2×314=2512cm 側面の面積=6cm×2512cm=cm 2 円柱の面積=5024cm 2 5024cm 2 cm 2 =2512cm 2
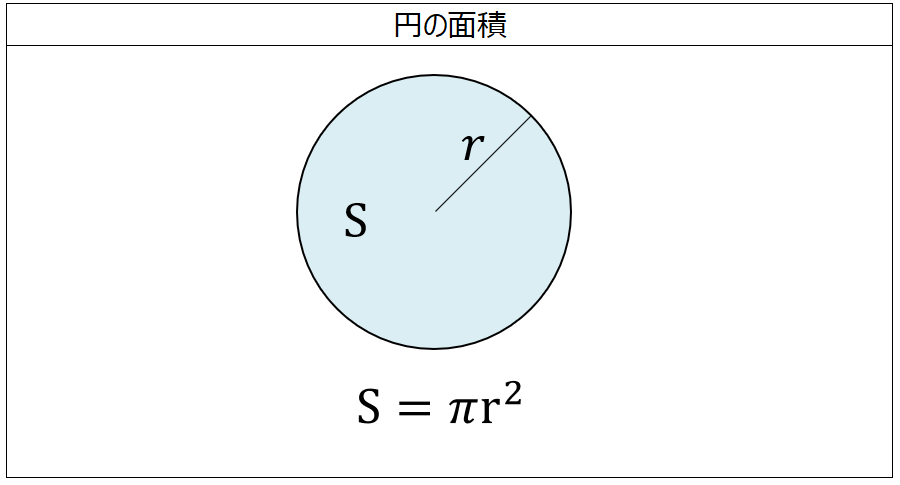
指定された面積を他の単位の面積に換算します。 サイトマップ 指定された面積を他の単位の面積に換算します。 計算したい面積と単位から他の単位の値を計算し表示します。円の面積は 半径×半径×円周率=面積 で求めることができます。 半径をr、円周率をπ、面積をSとすると S=πr 2 となります。円 面積計算 公式 求め方 計算方法 直径 半径 自動 円周率 計算機 履歴機能付き




半円や4分の1の円 四分円 の面積を計算する方法 モッカイ
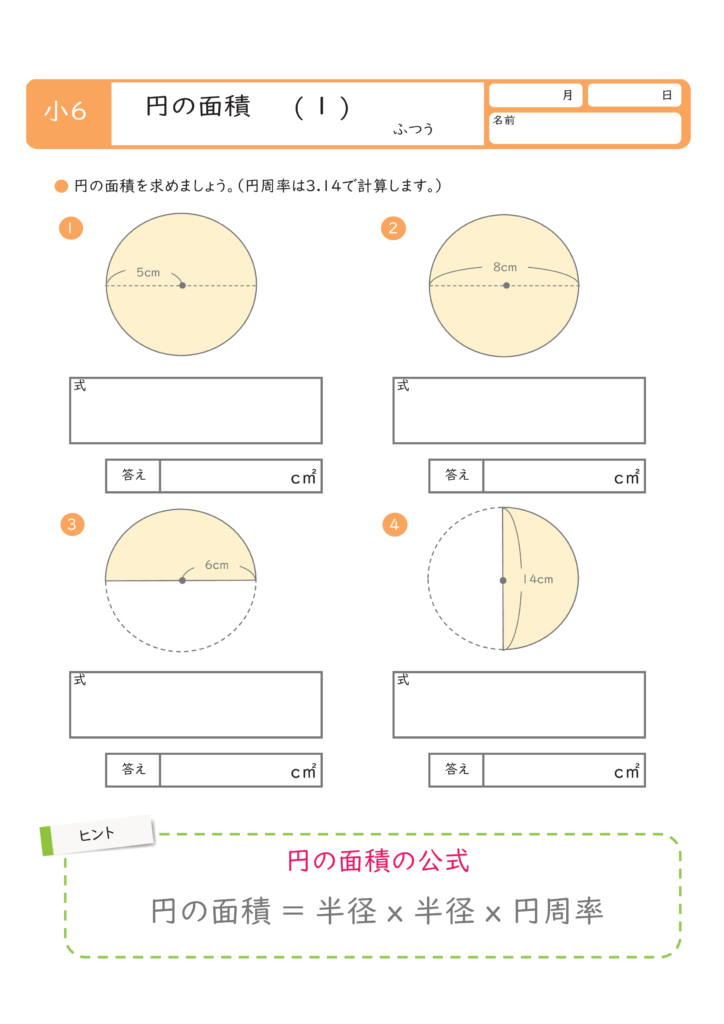



こどもプリント 円の面積 無料プリント
面積の計算ドリル 図形の面積をもとめよう 長方形,三角形,円,扇形,平行四辺形,台形などの図形の面積をもとめるドリルの作成プログラムです. 例によって数値の大きさを調整できます.数値が大きいと見にくくなる場合もあります.半径 x 半径 x 円周率今回は円なので、半径の大きさに注目しながら面積を求めてくださいね。 円の面積を忘れていた人は喝だッ! しっかりと思い出しておいてくださいね(_)/ これを計算していくと、



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note




小6 算数 小6 旧 円の面積 Youtube
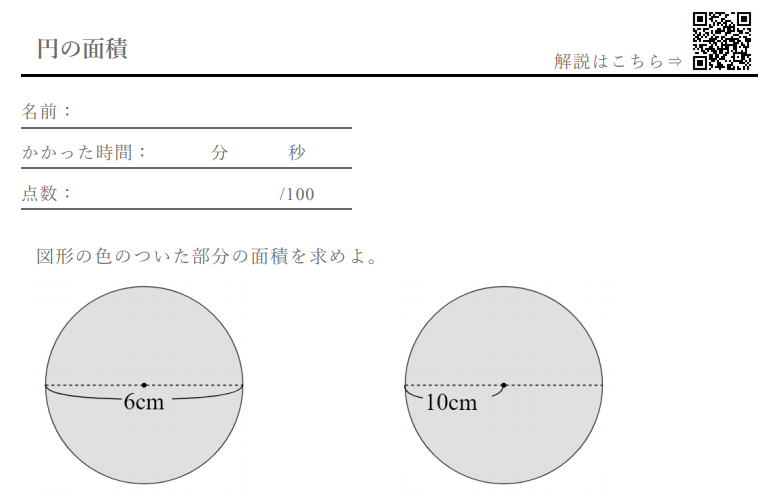
採点する やり直す 解説 3 半径 10 ,中心角が90°の扇形の面積 円の面積の4分の1だから,10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ,これから三角形の面積 10×10÷2=50 を引く円の面積を求める公式は、次の通りです。 円の面積 = 半径× 半径×314 円の面積 = 半径 × 半径 × 314スポンサーリンク 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 それでは「円の面積の公式」を使った「練習問題」を解いてみましょう。 練習問題① 半径が 2(cm)の円の面積を求めて



弓形の面積 弓形の半径と高さから 高精度計算サイト




土地家屋調査士 測量計算と面積計算 Amazon Com Books
求める面積を S とすると、 上式の定積分の計算は、置換積分を用いてもいいが、軽妙に「四分円の面積」から求め る方が多数だろう。 また、この楕円は、半径 倍縮小して得られるという性質を用い て、 πa 2 さらに、それぞれの円の扇形から三角形を引いたものを足せば赤色の面積が求められることが見えます。 図のように角度θ1、θ2を置くと、 s = ((円o1の角度θ1扇形の面積) (円o2の角度θ2扇形の面積) (三角形ao1o2の面積)) * 2 と求められます。 円の面積 半径 半径 円周率 円 の 面 積 = 半 径 × 半 径 × 円 周 率 = 4 × 4 × 314 = 5024 c m 2 と求まります。 問②面積が c m 2 の円の円周の長さを求めてください。 (円周率は 314 ) 円の面積の公式から半径を計算したあと 「半径⇒直径⇒円周の



おうぎ形 孤の長さ 面積は何倍か 計算しない 苦手な数学を簡単に
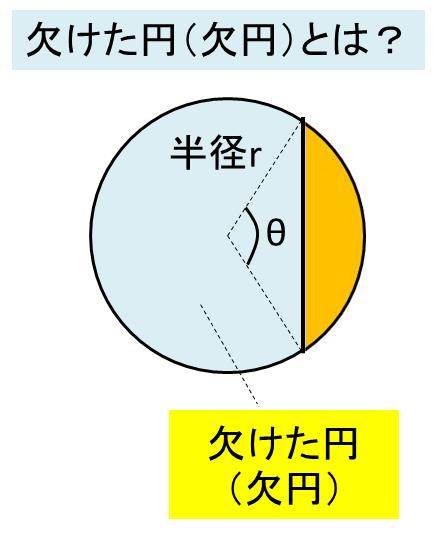



欠けた円 欠円 や弓形の面積の計算方法
公開 ・円の面積計算 半径と円周率(π)から円の面積を計算するプログラムを解説します。 円の面積は、半径×半径×円周率でで計算できます。 円周率は「π(パイ)」と呼ばれ、その値は で、小数点以下は無限に続きます。 ここでは、キーボードから半径を入力して、円円 円 半円 扇形 円周長から面積 四角形 四角形 四角形 4辺と対角線 角パイプ 三角形 三角形 三角形(3辺) 四角形 平行四辺形 ひし形 台形 lc形 l形 c形 円形 パイプ 楕円 長穴 多角形 六角形 八角形 その他 円 それぞれの面積を計算する前に,長さのわかる辺は長さを記入していまいましょう。 まずは, 直角三角形(水色) を計算すると 6×10÷2=60÷2=30cm² 上半分の四角形の面積は 6×16=96cm² おうぎ形 の中心角は90°で、面積は、円の面積の4分の1になるので 6




円の面積どこから計算すればいいのやら Clear



円の面積 算数の公式覚えてますか
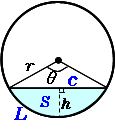
ただ、この公式。「半径 × 半径 × 314」が何をどう計算しているのか具体的にイメージしにくいという問題点があります。 「なんでこの公式で円の面積が求まるんだろう?」と感じる方も多いのではないでしょうか。正多角形の面積から辺と周の長を計算します。 円の面積 円の面積 半径から円の面積と円周を計算します。 円の面積から半径 円の面積から半径 円の面積sから半径、直径と円周を計算します。 扇形の面積 扇形の面積 扇形の半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。円盤に切り欠きを作る際には、計算するより前に切り欠きの幅を決めてしまいます。 ここから面積や重さを計算したいので、出来れば半径 r と弦の長さ c からの式を纏めて頂けると



断面積とは 1分でわかる求め方 長方形と円の公式 単位 計算方法 直径との関係



面積分
1 円の面積 右の図の扇形部分の面積に、その上の三角形の面積を加えればよいので h:l=1:0の意味なので、勾配I=1/0=0005と計算する。) 手順6 面積(流積)と潤辺から径深(R)を求める。→(式-3)直径Dから面積Aに変換する計算は「A=πD 2 /4」です。 円周率と直径の二乗を掛けて4で割った値です。 また、直径Dと半径rは「r=D/2」の関係です。 よって半径から面積に変換する計算式は「A=πr 2 」です。A=面積 楕 円 双 曲 線 放 物 線 (すなわちχを底辺としYを高さとする短形の面積の2/3に等しい) 放物線切片 サイクロイド




Excel エクセルで円の面積から直径を計算したり 直径から面積を求める方法 Pi関数の使用方法
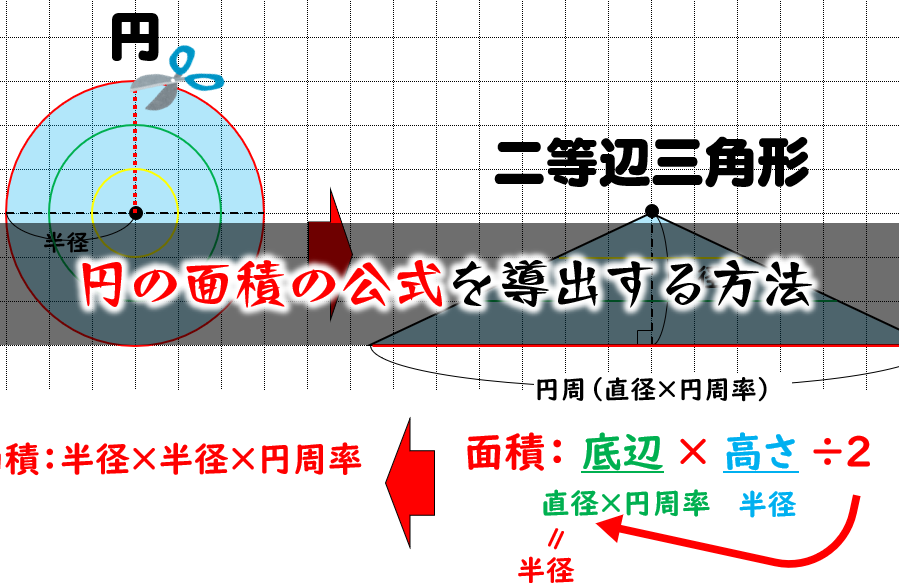



円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun
計算結果は問題ないのですが、参考の円弧の長さLの計算式 L=rθですが エクセルで半径×中心角とすると、計算の答えとエクセルの答えが違います。 どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角 小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色(かげ)がついた部分の面積の求め方全体白い部分円 A = 面積 D = 外径 d = 内径 楕円 A = 面積 P = 円周(近似式) 円錐 V = 体積 A = 円錐面積 r = d/2 = 半径 三角錐 V = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




円の面積の公式 算数の公式
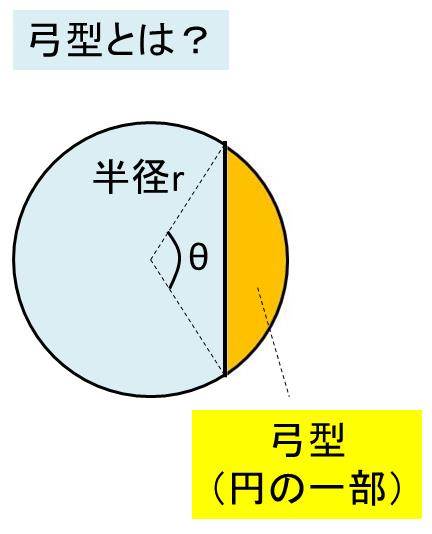



欠けた円 欠円 や弓形の面積の計算方法



円の面積 直径 半径 円周の計算機 公式を使った求め方も紹介 やまでら くみこ のレシピ



モンテカルロ法による円周率の計算



円と帯の共通部分の面積 Den Of Hardworking
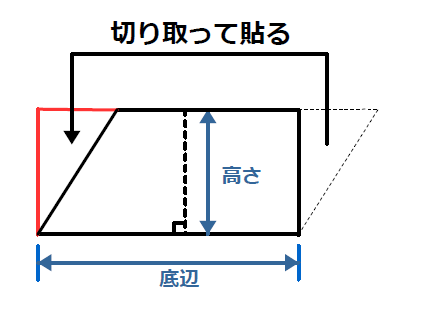



平行四辺形の面積計算 ゆるゆるプログラミング
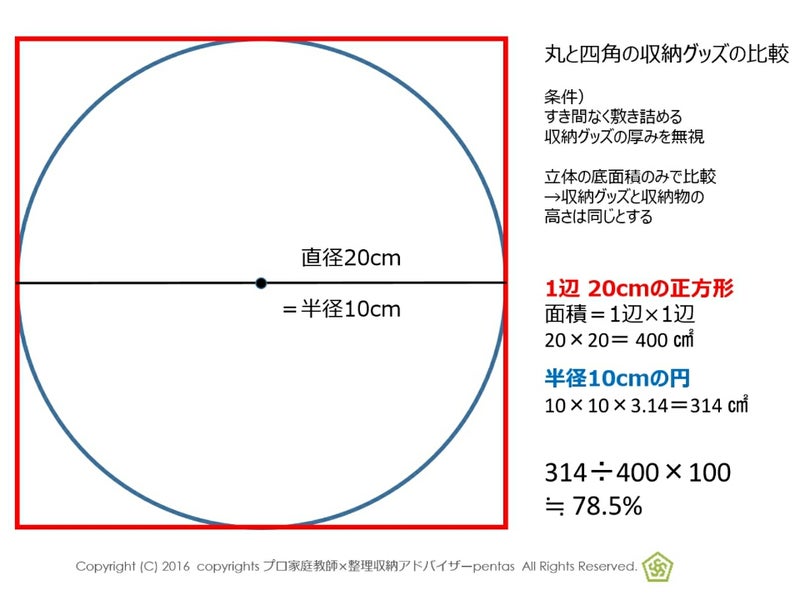



収納量の比較 数学の先生が 四角と丸の収納力を計算したら 中学受験から大学受験の塾プリント整理専門 プロ家庭教師 整理収納アドバイザー中島亜季 大阪京都奈良
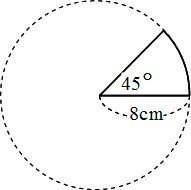



世界一やさしい 円の面積を求める問題の解き方 Shun Ei Note




Telecharger 面積計算アプリ 図形計算 Pour Iphone Sur L App Store Education




円の面積 算数用語集




中学数学 円の面積の求め方 の公式を1発で覚えてしまう裏技 Qikeru 学びを楽しくわかりやすく




面積の求め方 計算公式一覧



モンテカルロ法による円の面積計算




半円や4分の1の円 四分円 の面積を計算する方法 モッカイ
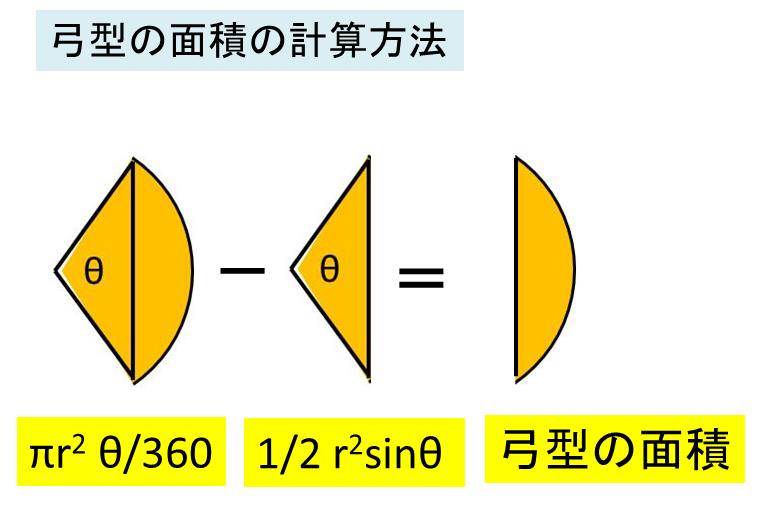



欠けた円 欠円 や弓形の面積の計算方法




小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




扇形の面積の求め方 公式と計算例
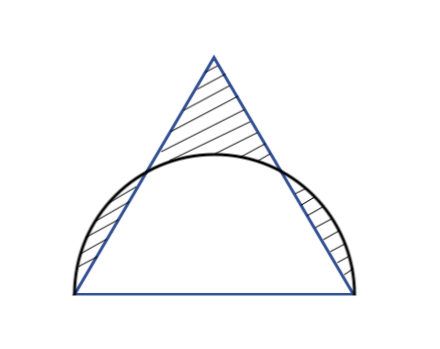



斜線部分の面積を求める問題 よくあるパターン 苦手な数学を簡単に
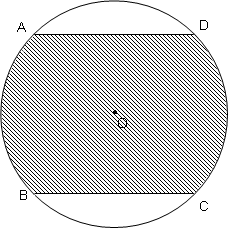



面積の求め方 算数の教え上手 学びの場 Com




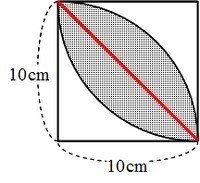
はっぱ型 の図形の面積 身勝手な主張




円の面積 円周の求め方 公式 小学生 中学生の勉強




小6 算数 小6 2 円の面積 応用編 Youtube
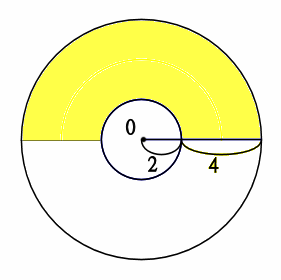



中のない円の面積
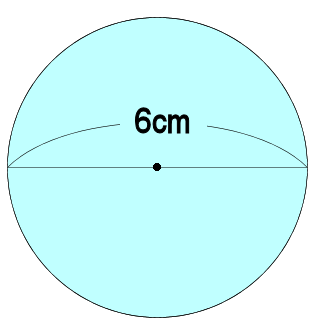



円の面積 直径
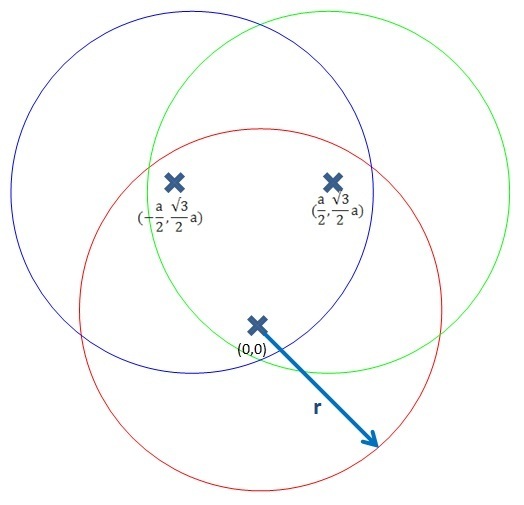



3つの円の共通部分の面積の数値計算 荒唐無稽で完全無欠の理想




円の面積と円周 計算機 半径や直径から計算 かんたん計算機




円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチニュース




面積の求め方 算数の教え上手 学びの場 Com




円の面積の求め方と覚えるコツ なぜ半径 半径 3 14になるか アタリマエ




Autocalc 長さ面積自動計算 Dans L App Store




円の面積の求め方を考えよう 小学校6年生の算数教材から 身勝手な主張




円 の面積 計算ドリル 問題集 数学fun




円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり




円の面積 練習応用 Youtube
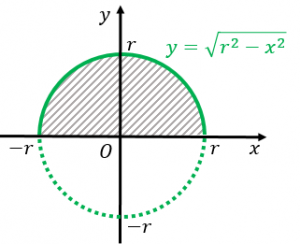



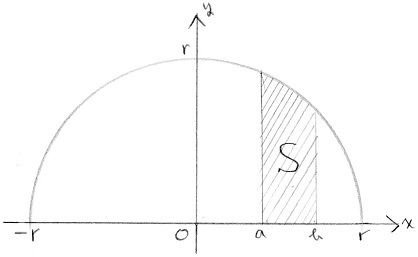
円の面積を積分で計算する2通りの方法 具体例で学ぶ数学
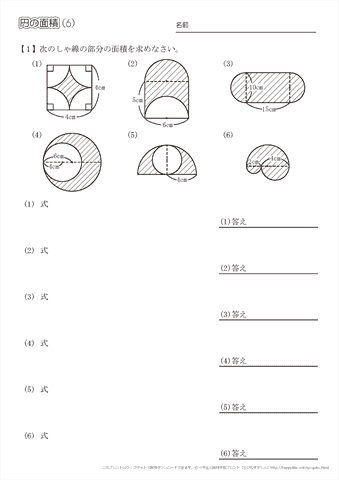



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生



面積の計算 円 製品設計知識
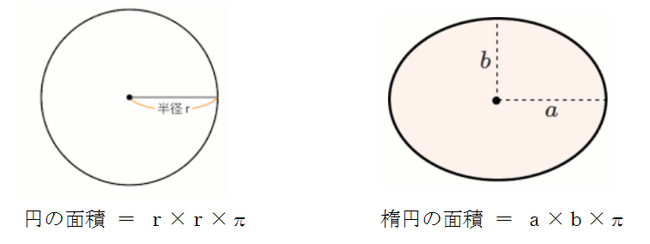



楕円の面積の公式 小学生でもわかる計算問題を紹介するぞ 三重の個人契約家庭教師



面白い円周率の歴史 昔の人たちはこうやって3 14 を求めてた 数学の面白いこと 役に立つことをまとめたサイト




円 扇形 の面積 周や弧の長さの公式 数学fun




面積計算アプリ 図形計算 By Takaaki Sasaki




円周の求め方の基本問題が解けるようになったら 次は応用問題にも挑戦してみましょう これも 5年生後半から6年生向けの内容です 円周の長さを求める応用問題を解こう 円周の長さを求める問題で もっと基本 数学ノート 学習 学習ノート




くろべえ 卵焼きの失敗と 2円の重なり部分の面積
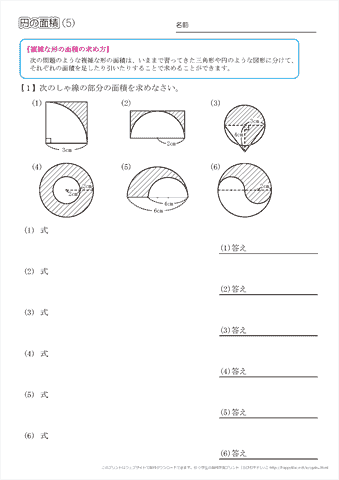



小学6年生の算数 円の面積 問題プリント ちびむすドリル 小学生




円の面積の求め方 公式と計算例



1
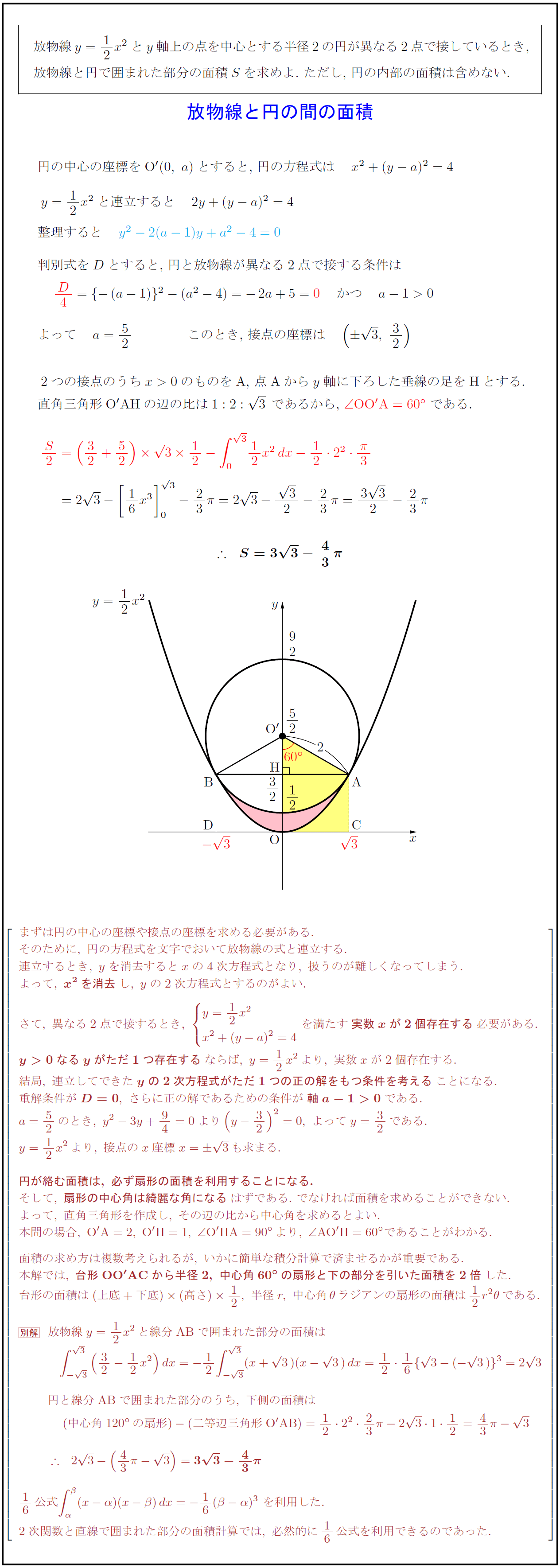



高校数学 放物線と円の間の面積 受験の月




楕円の面積と楕円体の体積の求め方 宇宙に入ったカマキリ



Math Battle 0098 簡単な面積計算




円の面積の求め方 公式と計算例
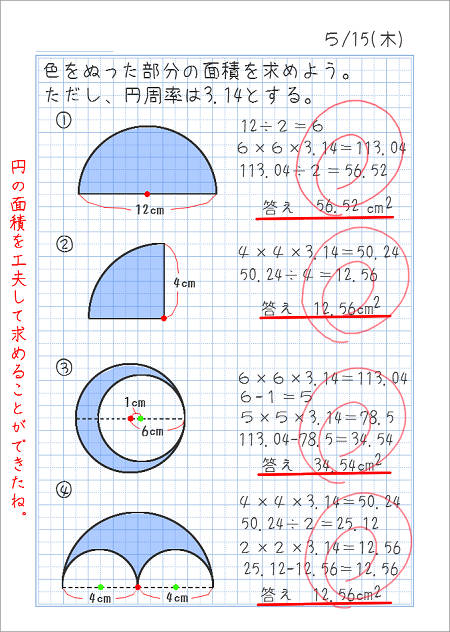



円の面積 その1 家庭学習レシピ




プログラミング モンテカルロ法による面積計算 理系のための備忘録
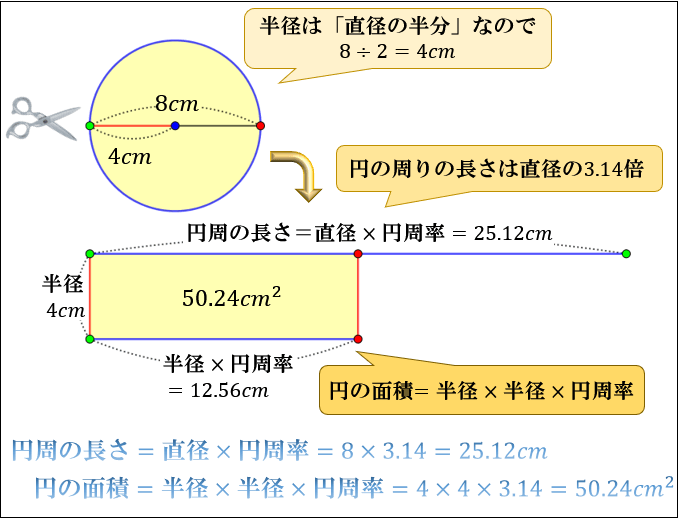



円周の求め方と円の面積について アタリマエ



問題93おうぎ形の面積




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく



円を直線で切った時の面積の計算方法を教えてください 半径rの円の一 Yahoo 知恵袋



1
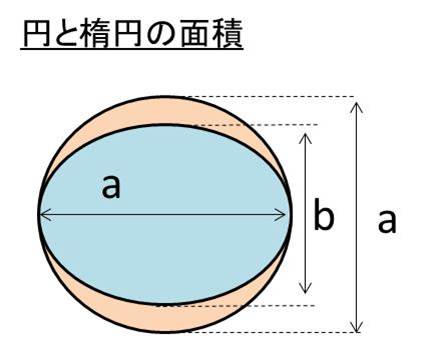



X Acos8とy Bsin8の面積の計算方法は 楕円の面積の一部の求め方は 楕円の面積と円の面積 ウルトラフリーダム
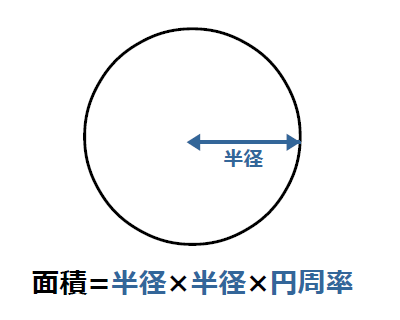



円の面積計算 ゆるゆるプログラミング




円の面積の公式 円周の求め方と間違えないようにしよう 中学や高校の数学の計算問題




Android 用の 面積計算 Bynsdev Apk をダウンロード



Q Tbn And9gctj3goo5njmuwc 7pm2d T9knxkls8ofsc90dliywxdejwyqaiv Usqp Cau



多角形の面積で円周率を求める Allisone




円周の求め方と円の面積について アタリマエ




円の面積の公式 なぜ半径と円周率で求められるのか を小学生に分かりやすく説明する方法 数学fun



Excelで操る 円の面積計算 楕円の面積計算
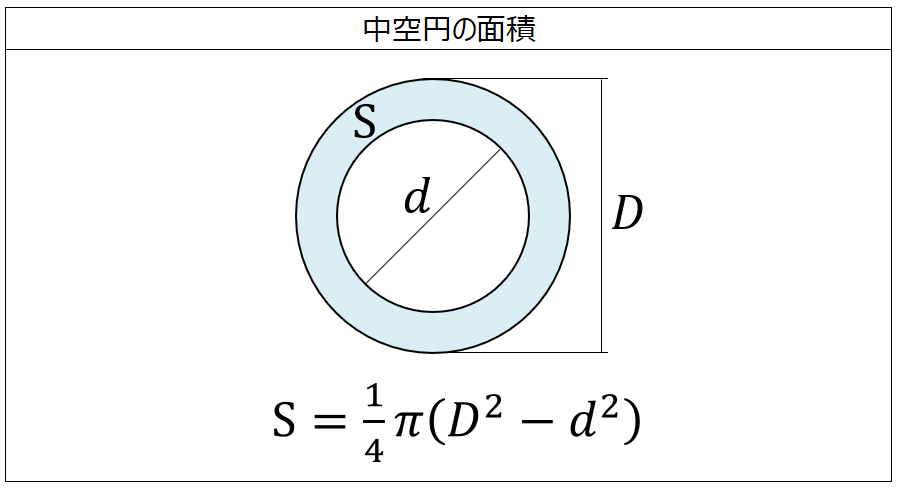



面積の計算 中空円 製品設計知識



円の面積と周長




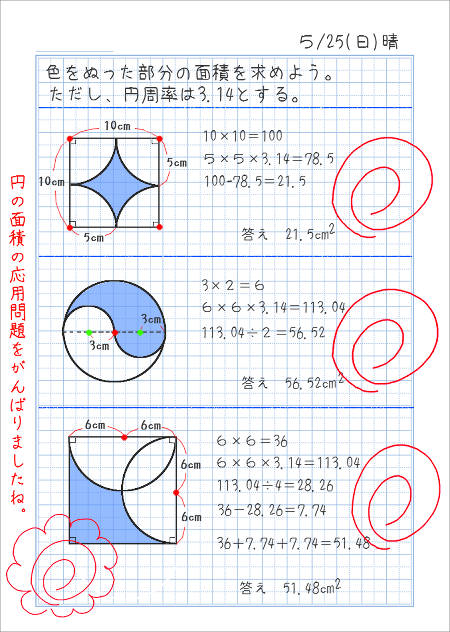
円の面積の応用 小学校6年算数より 身勝手な主張



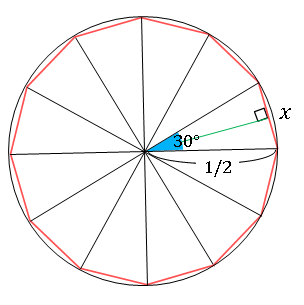
円の相似を利用した面積の計算 中学受験プロ講師ブログ



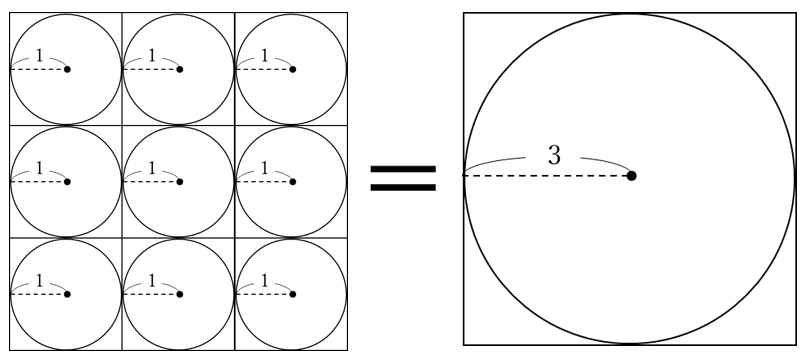
円の面積 その2 家庭学習レシピ
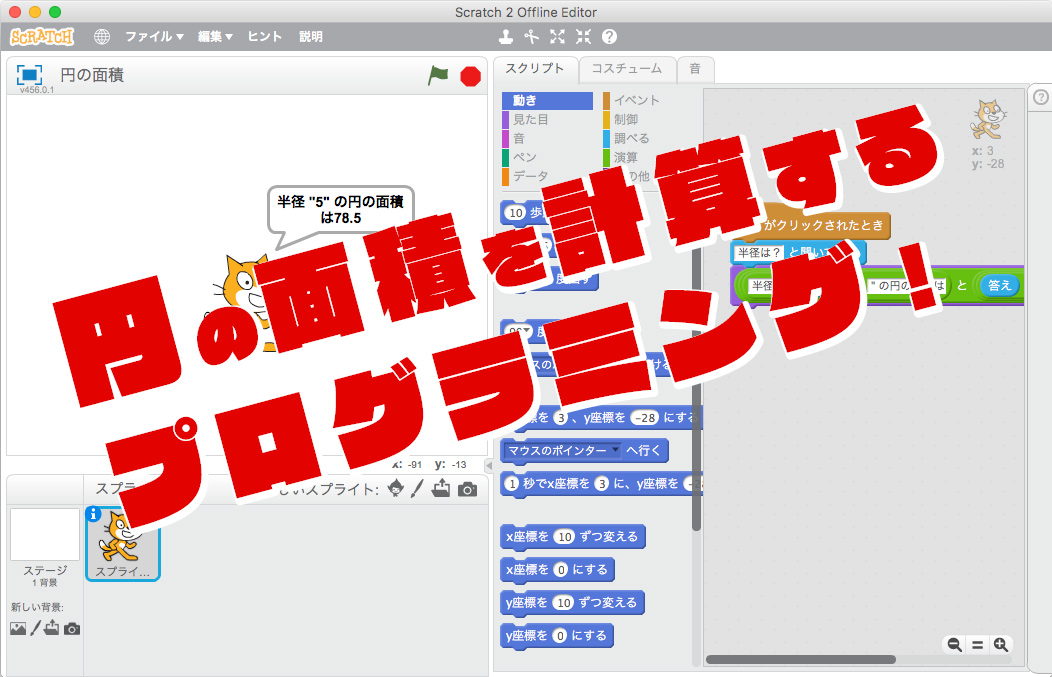



Scratchで作る 円の面積を計算するプログラミングを作ろう 子供 小学生のオンラインプログラミング教室 アンズテック



1



円の面積と公式 面積計算機
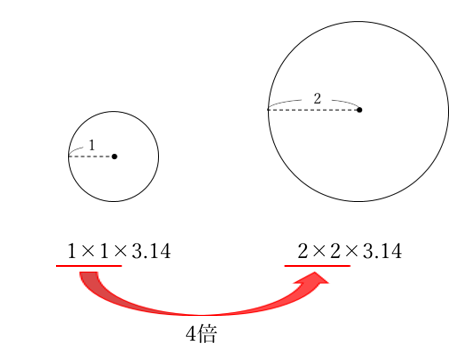



円の相似を利用した面積の計算 中学受験プロ講師ブログ
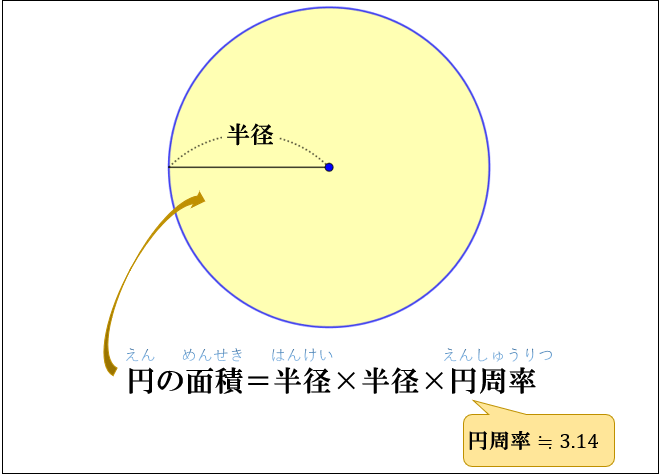



円周の求め方と円の面積について アタリマエ
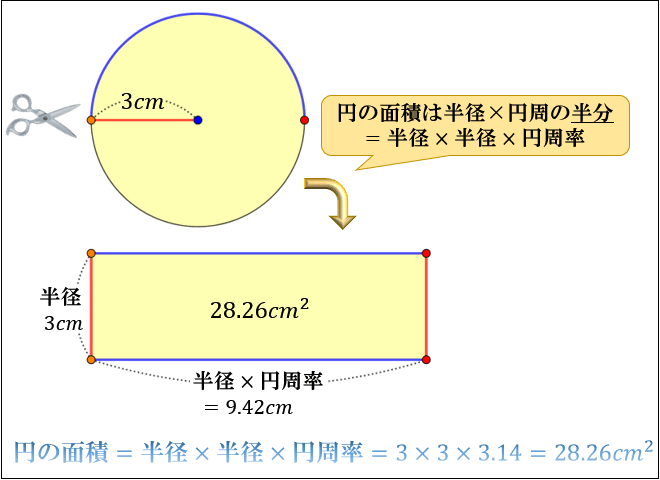



円周の求め方と円の面積について アタリマエ



学習ポスター 面積の計算 公式表 部屋用 小学生 算数 A5サイズ Hhgp Ss0004 サンライズ長野yahoo ショップ 通販 Yahoo ショッピング
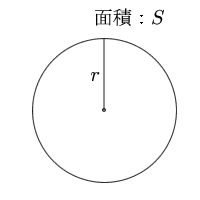



円 面積の計算 計算サイト



楕円の面積の計算 自動計算サイト




ボード 子供に教えること のピン



円の面積 簡単に計算できる電卓サイト




円の面積の求め方 公式と計算例
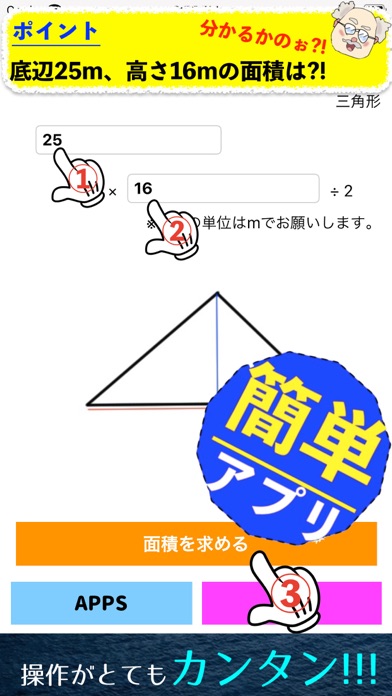



Telecharger 面積計算アプリ 図形計算 Pour Iphone Sur L App Store Education
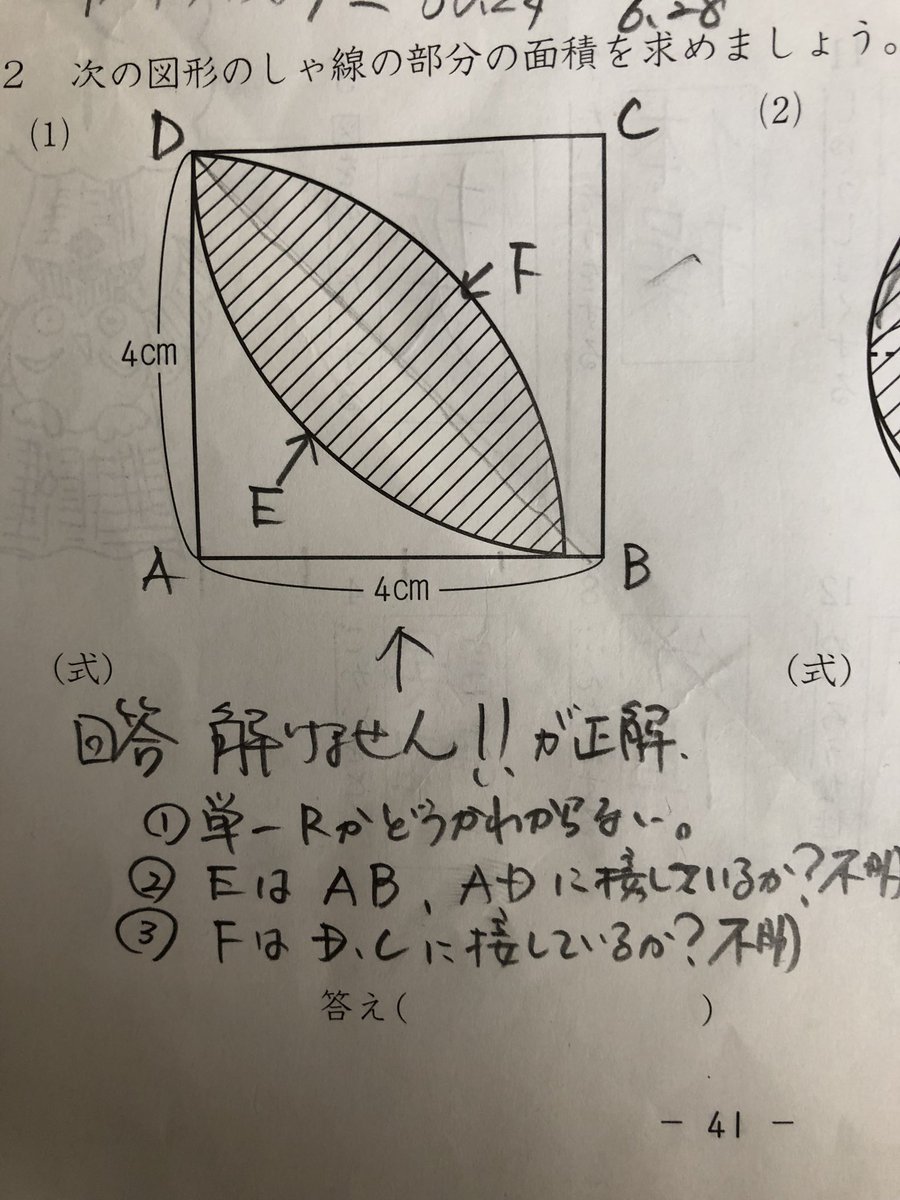



円の面積




勉強しよう数学 円の面積を積分で求める




Telecharger 面積計算アプリ 図形計算 Pour Iphone Sur L App Store Education
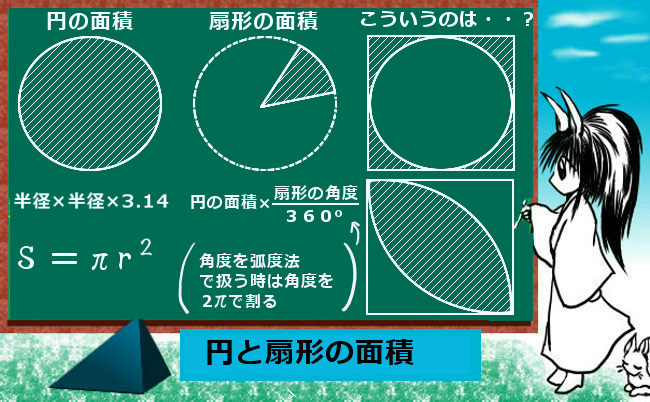



円 扇形に関連する面積の計算 理数系無料オンライン学習 Kori
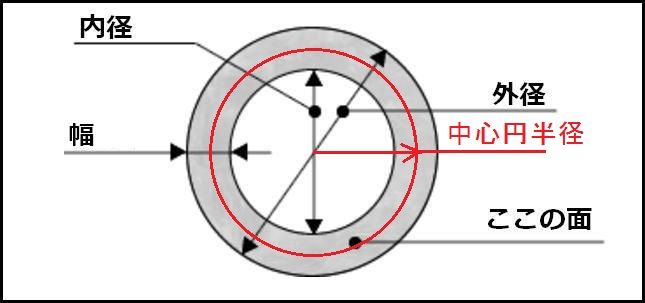



円に関する計算式のまとめ 機械設計メモ



0 件のコメント:
コメントを投稿